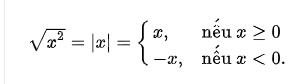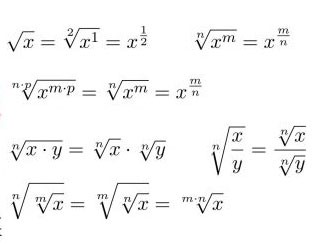الجذر التربيعي، كيفية حساب الجذر التربيعي

يعتبر الجذر التربيعي أحد المعارف المهمة في الرياضيات والتي تستخدم في عملية التعلم للطلاب. المقال التالي سوف يقدم لك تعريف الجذر التربيعي وكيفية حساب الجذر التربيعي لعدد ما؟ يرجى الرجوع إلى.

جدول المحتويات

• ما هو الجذر التربيعي؟
• أبسط حسابات الجذر التربيعي
  • جدول الجذر التربيعي
• كيفية حساب الجذر التربيعي بدون استخدام الآلة الحاسبة
  • إيجاد الجذر التربيعي لعدد صحيح
  • إيجاد الجذر التربيعي للأرقام الأخرى
• كيفية مقارنة الجذور التربيعية 

ما هو الجذر التربيعي؟

الجذر التربيعي للعدد a هو العدد x بحيث x2 = a، أو بمعنى آخر، العدد x الذي قيمته التربيعية = a.

على سبيل المثال، 2 و−2 هما الجذر التربيعي لـ 2 لأن 2² = (−2)² = 4.

يتم الإشارة إلى علامة الجذر بواسطة √.

• كل عدد حقيقي غير سلبي a له جذر مربع غير سلبي فريد، يسمى الجذر التربيعي الحسابي.

على سبيل المثال، الجذر التربيعي الحسابي لـ 16 هو 4، ويرمز له بـ √16 = 4، لأن 4² = 4 × 4 = 16 و4 هو عدد غير سلبي.

كل عدد موجب a له جذرين مربعين: √a هو جذر مربع موجب و −√a هو جذر مربع سالب. يتم الإشارة إليهما في نفس الوقت بـ ± √a.

أبسط حسابات الجذر التربيعي

تذكر بعض الأرقام التربيعية الأساسية والأكثر شيوعًا حتى تتمكن من الحساب بشكل أسرع في ذهنك عند أخذ الجذر التربيعي:

0² = 0
1² = 1
3² = 9
4² = 16
5² = 36 7² = 49
8² =
64
9² =
81 10² =
100
11² = 121 12²
= 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289

تتضمن بعض صيغ الجذر التربيعي الأساسية التي يجب على الجميع تذكرها ما يلي:

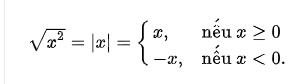
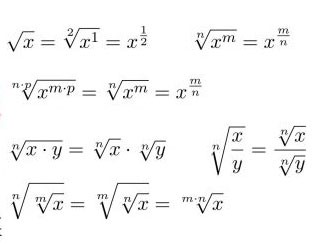
جدول الجذر التربيعي

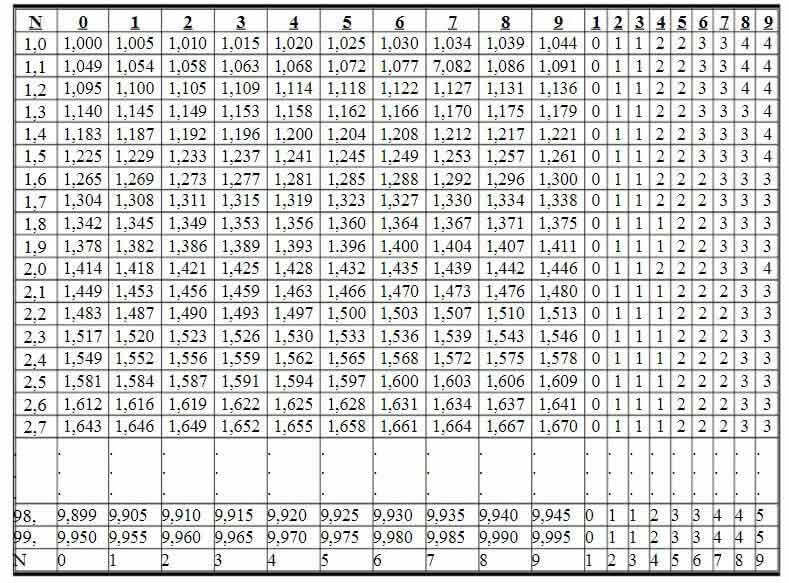
يتم تقسيم جدول الجذر التربيعي إلى صفوف وأعمدة، مما يسمح بالعثور مباشرة على الجذر التربيعي للأرقام الأكبر من 1 والأقل من 100.

يتم إعطاء الجذور التربيعية للأعداد المكتوبة بما لا يزيد عن ثلاثة أرقام من 1.00 إلى 99.9 في الجدول في الأعمدة من 0 إلى 9. بعد ذلك توجد تسعة أعمدة تصحيح تُستخدم لتصحيح الرقم الأخير من الجذور التربيعية للأعداد المكتوبة بأربعة أرقام من 1.000 إلى 99.99.

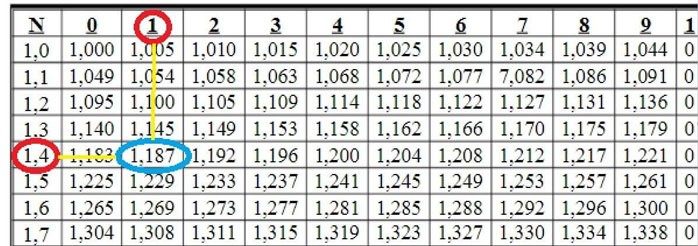
مثال 1: البحث

→ الحل:

عند تقاطع الصفوف 1 و 4 والعمود 1 نرى الرقم 1187

لذا

مثال 2: 

يجد

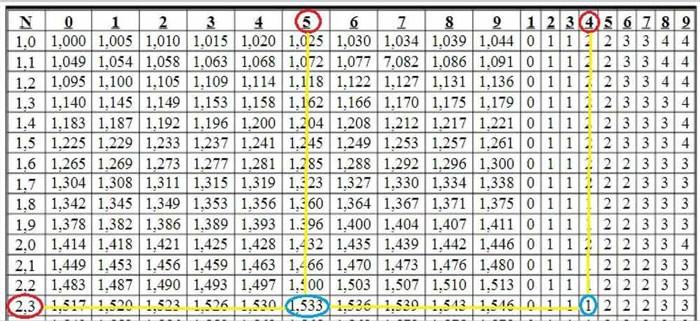
في تقاطع الصفوف 2،3 والعمود 5 نرى الرقم 1.533. لدينا

بعد ذلك، عند تقاطع الصفوف 2 و3 والعمود 4، نرى الرقم 1. ويُستخدم هذا الرقم 1 لتصحيح الرقم الأخير في العدد. أي: 1.533 + 0.001 = 1.534

لذا

كيفية حساب الجذر التربيعي بدون استخدام الآلة الحاسبة

إيجاد الجذر التربيعي لعدد صحيح

إيجاد الجذر التربيعي عن طريق الضرب.

الجذر التربيعي لرقم هو الرقم الذي عندما تضربه في نفسه يعطيك الرقم الأصلي.

وهذا يعني "ما هو الرقم الذي يمكنك ضربه في نفسه للحصول على الرقم الذي لديك بالفعل؟"

على سبيل المثال:

الجذر التربيعي لـ 1 هو 1 لأن 1 × 1 يساوي 1 (1 × 1 = 1).

الجذر التربيعي لـ 4 هو 2 لأن 2 × 2 يساوي 4 (2 × 2 = 4).

الجذر التربيعي لـ 9 هو 3 لأن 3 × 3 = 9.

استخدم القسمة لإيجاد الجذر التربيعي

للعثور على الجذر التربيعي لعدد صحيح، يمكنك قسمة العدد الصحيح على أرقام متتالية حتى تجد حاصل قسمة مطابق تمامًا للمقسوم عليه.

على سبيل المثال:

16 مقسومًا على 4 يساوي 4، وبالتالي فإن 4 هو الجذر التربيعي لـ 16.

4 مقسومًا على 2 يساوي 2، لذا فإن 2 هو الجذر التربيعي لـ 4.

إيجاد الجذر التربيعي للأرقام الأخرى

خمن ثم استخدم عملية الإقصاء.

مثال: إيجاد الجذر التربيعي لـ 20.

وفي الوقت نفسه، نعلم أن 16 هو عدد مربع كامل مع الجذر التربيعي لـ 4 (4X4 = 16).

25 لديه أيضًا الجذر التربيعي لـ 5 (5X5 = 25).

لذا فإننا نخمن أن الجذر التربيعي لـ 20 سيكون في مكان ما بين 4 و 5.

يمكننا أن نخمن أن الجذر التربيعي لـ 20 هو 4.5 ونحاول تربيع 4.5 للتأكد. أي نأخذ 4.5 × 4.5، إذا كانت الإجابة ليست 20، ثم نرى هل النتيجة أكبر من أو أقل من 20 للحساب. إذا كان أقل من 20، فإننا نستمر في المحاولة مع 4 و6 وأعداد أكبر. إذا كانت النتيجة أكبر من 20، فحاول الحساب باستخدام 4 و4 وأرقام أصغر حتى تحصل على النتيجة الصحيحة.

النتيجة في هذا الحساب هي 4.475 × 4.475 = 20.03. عندما تقوم بالتقريب للأسفل، فإن الإجابة هي 20.

كيفية مقارنة الجذور التربيعية

مع أي عددين موجبين a و b

إذا كان أ = ب فإن

إذا كان أ > ب فإن

إذا كان <b="" then="">

على سبيل المثال: 

قارن و

لأن 21 < 31،

نأمل أن تكون المقالة أعلاه قد ساعدتك في فهم المعرفة حول الجذور التربيعية، وكيفية الحساب، وكيفية المقارنة... لحل التمارين حول الجذور التربيعية بالإضافة إلى التمارين الأخرى ذات الصلة.