صيغة حساب الارتفاع في المثلث المنتظم، والمتساوي الساقين، والمتساوي الأضلاع، والمثلث القائم الزاوية

الارتفاع في المثلث هو خط مستقيم له خصائص مهمة وهو مرتبط ارتباطًا وثيقًا بمشكلات الهندسة المستوية. فما هو الارتفاع، وكيف نحسب الارتفاع في المثلث؟ يرجى الرجوع إلى المقال أدناه للحصول على الإجابة والصيغة الأبسط لحساب ارتفاع المثلث.

جدول المحتويات

• صيغة حساب الارتفاع في المثلث
  • حساب الارتفاع في مثلث منتظم
  • حساب الارتفاع في مثلث متساوي الأضلاع
  • صيغة حساب الارتفاع في المثلث القائم
  • صيغة حساب الارتفاع في مثلث متساوي الساقين
• تعريف الارتفاع في المثلث
• خصائص الارتفاعات الثلاثة للمثلث

صيغة حساب الارتفاع في المثلث

حساب الارتفاع في مثلث منتظم

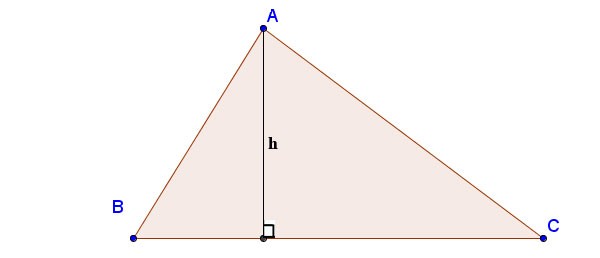
كيفية حساب ارتفاع المثلث باستخدام صيغة هيرون:

حيث أن أ، ب، ج هي أطوال الأضلاع؛ ha هو الارتفاع المرسوم من الرأس A إلى الجانب BC؛ p هو نصف المحيط:

على سبيل المثال: 

المثلث ABC، الضلع AB = 4 سم، الضلع BC = 7 سم، الضلع AC = 5 سم. احسب الارتفاع AH من A المتقاطع مع BC عند H واحسب مساحة ABC.

جائزة:

نصف محيط المثلث: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(سم)

ارتفاع   

=>

انظر إلى المثلث ABC، لدينا:

لذا،

حساب الارتفاع في مثلث متساوي الأضلاع

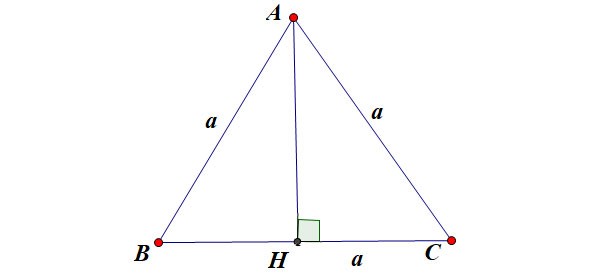
افترض أن المثلث المتساوي الأضلاع ABC له طول ضلع a كما هو موضح في الشكل:

هناك:

• h هو ارتفاع المثلث المتساوي الأضلاع
• أ هو طول ضلع المثلث المتساوي الأضلاع

صيغة حساب الارتفاع في المثلث القائم

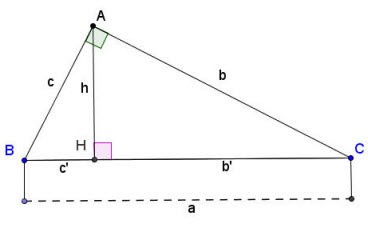
افترض أن هناك مثلث قائم الزاوية ABC عند النقطة A كما هو موضح أعلاه:

صيغة حساب الأضلاع والارتفاعات في المثلث القائم:

1. أ2 = ب2 + ج2

2. b2 = ab′ و c2 = ac′

3. آه = قبل الميلاد

4. h2 = b′.c'

5.

هناك:

• أ، ب، ج هي أضلاع المثلث القائم كما هو موضح أعلاه؛
• b' هو إسقاط الحافة b على الوتر؛
• c' هو إسقاط الحافة c على الوتر؛
• h هو ارتفاع المثلث القائم الزاوية المرسوم من رأس الزاوية القائمة A إلى الوتر BC.

مثال 1: المثلث ABC قائم الزاوية في A، وارتفاعه AH. احسب BC وAC وAH مع العلم أن AB = 15 سم وHC = 16 سم.

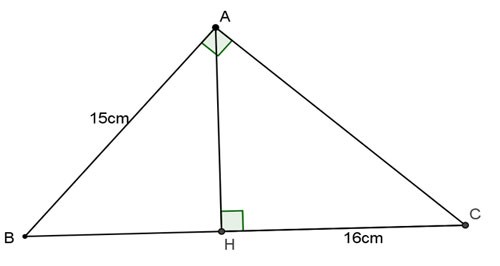
جائزة:

بتطبيق الصيغة الجبرية في المثلث القائم ABC نحصل على:

AC2 = CH.BC = 16.BC

وفقًا لنظرية فيثاغورس للمثلث القائم ABC والزاوية القائمة A لدينا:

AB2 + AC2 = BC2

⇔ 152 + 16.قبل الميلاد = قبل الميلاد2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ ق(ق - 25) + 9 (ق - 25) = 0

⇔ (قبل الميلاد - 25)(قبل الميلاد + 9) = 0

⇔ BC = 25 أو BC = -9 (حذف)

⇒ AC2 = 16.BC = 16.25 = 400 ⇒ AC = 20 (سم)

لنفترض أن المثلث القائم ABC هو: AH.BC = AB.AC (الصيغة الهندسية)

=> AH = AB.AC/BC = 15.20/25 = 12 (سم)

لذا BC=25(سم)؛ التيار المتردد=20(سم)؛ أه = 12 (سم)

مثال 2 :

إذا كان المثلث ABC قائم الزاوية في A، فإن AB=24cm، AC=32cm. يتقاطع المنصف العمودي لـ BC مع AC وBC في D وE على التوالي. احسب DE.

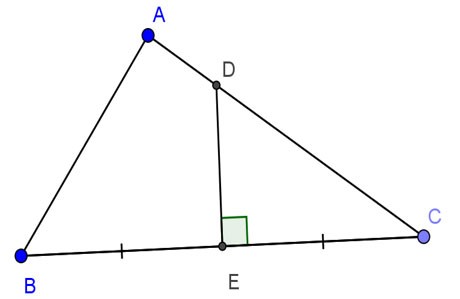
جائزة:

نأخذ في الاعتبار المثلث القائم ABC، لدينا:

BC2 = AB2 + AC2 (وفقًا لنظرية فيثاغورس)

BC2 = 242+ 322

BC2 = 1600

ق م = 40(سم)

EC = BC : 2 = 40 : 2 = 20(سم)

خذ في الاعتبار المثلث القائم ACB والمثلث القائم ECD مع:

هناك ∠A = ∠E = 90o

∠C مشترك

=> مثلث ACB ∾ مثلث ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15 سم

لذا ED = 15 سم

صيغة حساب الارتفاع في مثلث متساوي الساقين

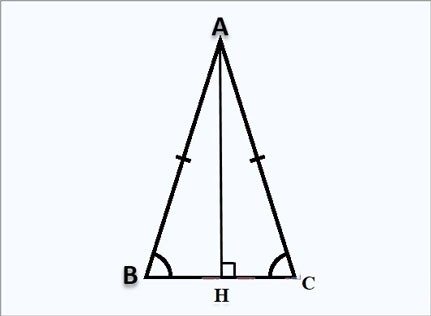
افترض أن لديك مثلث متساوي الساقين ABC عند A، وارتفاع AH عمودي عند H كما هو موضح أعلاه:

صيغة حساب الارتفاع AH:

نظرًا لأن المثلث ABC متساوي الساقين عند A، فإن الارتفاع AH هو المتوسط ​​أيضًا، لذا:

⇒ HB=HC= ½BC

بتطبيق نظرية فيثاغورس في المثلث القائم الزاوية ABH عند H نحصل على:

AH²+BH²=AB²

⇒AH²=AB²−BH²

على سبيل المثال : إذا كان Δ ABC متوازنًا عند A حيث BC = 30 (سم)، والارتفاع AH = 20 (سم). احسب الارتفاع المقابل لضلع المثلث المتساوي الساقين.

الحل: افترض أن Δ ABC متساوي الساقين عند A مع BC = 30(سم)

⇒ BH = CH = 15(سم).

بتطبيق نظرية فيثاغورس لدينا:

الآن علينا أن نحسب BK = ؟

لدينا:

على الجانب الآخر

لذلك لدينا ⇔

تعريف الارتفاع في المثلث

الارتفاع في المثلث هو قطعة عمودية مرسومة من رأس إلى الجانب المقابل. يُطلق على الجانب المقابل اسم القاعدة المقابلة للارتفاع. طول الارتفاع هو المسافة بين الأعلى والأسفل.

خصائص الارتفاعات الثلاثة للمثلث

تمر ارتفاعات المثلث الثلاثة عبر نفس النقطة. وتسمى هذه النقطة بمركز تقويم المثلث .

كل ما عليك فعله هو حساب المكونات المجهولة في الصيغ أعلاه لحساب ارتفاع المثلث لتتمكن من حساب ارتفاع المثلث.

• ما هو التركيز؟ صيغة حساب مركز ثقل المثلث