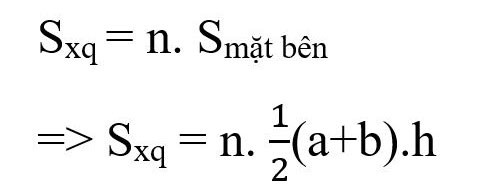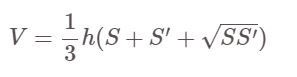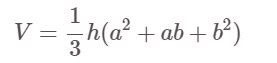صيغة حساب حجم الهرم المقطوع والمساحة الجانبية والمساحة الكلية للهرم المقطوع

دعونا نتعلم ما هو الهرم المقطوع، وكيفية حساب حجم الهرم المقطوع، والمساحة الجانبية والمساحة الكلية للهرم المقطوع في المقال أدناه.

جدول المحتويات

• تعريف المخروط الناقص
  • خصائص الهرم المقطوع:
• صيغة حساب مساحة الهرم المقطوع
  • مساحة سطح الهرم المقطوع 
  • المساحة السطحية الكلية للهرم المقطوع
• صيغة حساب حجم الهرم المقطوع

تعريف المخروط الناقص

الهرم المقطوع هو جزء من متعدد السطوح، يقع بين القاعدة والمقطع العرضي المقطوع بواسطة مستوى موازٍ لقاعدة الهرم.

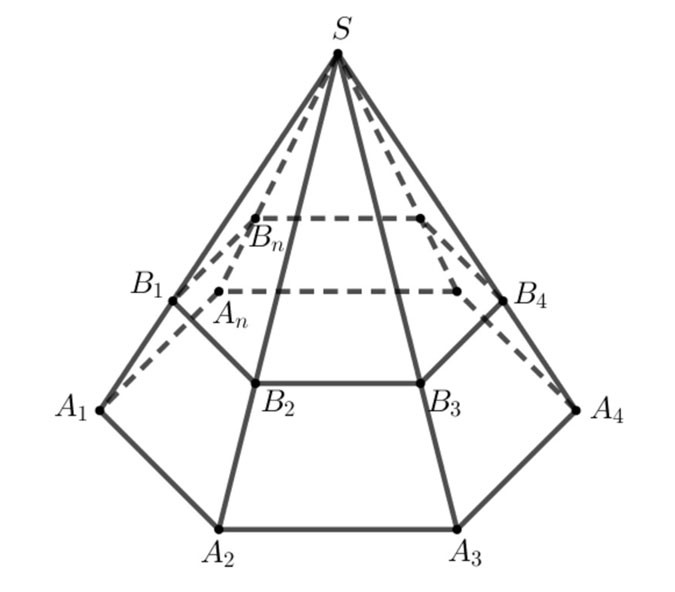
• الشكل الذي يتكون من مضلعات A1A2...An،B1B2...BnA1A2...An،B1B2...Bn وشبه منحرف A1A2B2B1،A2A3B3B2،...،AnA1B1BnA1A2B2B1،A2A3B3B2،...،AnA1B1Bn يسمى هرمًا مقطوعًا، ويشار إليه بـ A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
• ببساطة، يتكون الهرم المقطوع من الهرم S.A1A2...AnS.A1A2...An بعد قطع الهرم S.B1B2...Bn.S.B1B2...Bn.

+ المضلعات A1A2...An،B1B2...BnA1A2...An،B1B2...Bn تسمى القاعدتين،

+ تُسمى الأشكال شبه المنحرفة A1A2B2B1،A2A3B3B2،...،AnA1B1BnA1A2B2B1،A2A3B3B2،...،AnA1B1Bn بالوجوه الجانبية.

+ تسمى أجزاء الخط A1B1، A2B2،...، AnBnA1B1، A2B2،...، AnBn بالحواف الجانبية، وتسمى حواف سطح القاعدة بالحواف الأساسية.

+ المسافة بين القاعدتين تسمى ارتفاع الهرم المقطوع.

خصائص الهرم المقطوع:

• القاعدتان هما مضلعان (مثلثات، رباعيات، خماسيات، إلخ) مع أضلاع متوازية متناظرة ونسب متساوية من الأضلاع المتناظرة.
• الوجوه الجانبية كلها على شكل شبه منحرف.
• ستتقارب الخطوط التي تحتوي على الحواف الجانبية عند نقطة واحدة (أعلى الهرم).
• الهرم المقطوع هو هرم تكون قواعده عبارة عن مضلعات منتظمة (بأضلاع متساوية). لذلك، فإن الوجوه الجانبية للمخروط الناقص هي كلها شبه منحرف متساوية.

صيغة حساب مساحة الهرم المقطوع

مساحة سطح الهرم المقطوع

المساحة الجانبية للهرم المقطوع هي مساحة الوجوه المحيطة، أي الجزء المحيط بالهرم المقطوع، باستثناء مساحة القاعدتين.

كيفية حساب المساحة الجانبية للهرم المقطوع: احسب مساحة كل وجه جانبي (شبه منحرف) للهرم المقطوع حسب صيغة حساب مساحة شبه المنحرف الطبيعي ، ثم احسب المساحة الكلية.

صيغة حساب مساحة الهرم المقطوع المنتظم:

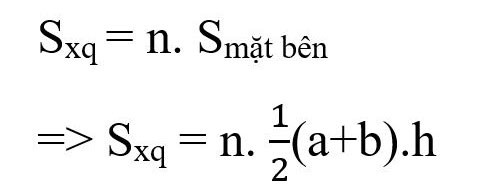
هناك:

• Sxq: المنطقة المحيطة
• ن: عدد الوجوه الجانبية للهرم المقطوع (يساوي عدد حواف المضلع القاعدي)
• أ، ب: أطوال أضلاع القاعدتين العلوية والسفلية على التوالي
• ح: ارتفاع ضلع المربع.

مثال 1: 

احسب المساحة الجانبية لهرم رباعي منتظم مقطوع طول قاعدته 10سم وطول ضلعه 15سم وارتفاع ضلعه 12سم.

جائزة: 

الوجه الجانبي للهرم الرباعي المقطوع المنتظم هو شبه منحرف متساوي الساقين، وبالتالي فإن مساحة أحد الوجوه الجانبية هي:

يحتوي الهرم الرباعي المقطوع المنتظم على 4 أضلاع متساوية، وبالتالي فإن مساحته الجانبية هي:

150 × 4 = 600 (سم2)

مثال 2: احسب المساحة الجانبية لهرم رباعي منتظم مقطوع طول قاعدته 6سم وطول ضلعه 8سم وارتفاع ضلعه 5سم. احسب المساحة الجانبية لهرم رباعي منتظم مقطوع قاعدته 6سم وطول ضلعيه 8سم.

جائزة: 

الوجه الجانبي للهرم الرباعي المقطوع المنتظم هو شبه منحرف متساوي الساقين، وبالتالي فإن مساحة أحد الوجوه الجانبية تساوي

يحتوي الهرم الرباعي المقطوع المنتظم على أربعة أضلاع متساوية وبالتالي فإن مساحته الجانبية تساوي

35 × 4 = 140 (سم2)

المساحة السطحية الكلية للهرم المقطوع

المساحة الكلية للهرم المقطوع تساوي مجموع المساحة الجانبية ومساحة القاعدتين.

الصيغة:                    Stp = Sxq + القاع الكبير + القاع الصغير

هناك:

• Stp: المساحة الكلية
• Sxq: المنطقة المحيطة
• قاعدة كبيرة: مساحة قاعدة كبيرة
• قاعدة صغيرة: مساحة قاعدة صغيرة

على سبيل المثال: 

احسب المساحة الكلية للهرم المقطوع المنتظم حسب الأبعاد الموضحة في الشكل.

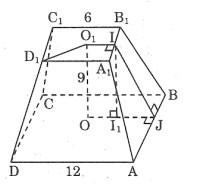
جائزة:

لدينا:

AD = 12 ⇒ OJ = 6

ارسم II1 ⊥ OJ لدينا: I1J = 3

بتطبيق نظرية فيثاغورس على المثلث القائم II1J لدينا:

IJ2 = II12 + I1J2 = 92 + 32 = 90

لذلك:

مساحة أحد أضلاع شبه المنحرف هي:

المساحة المحيطة تساوي:

مساحة القاعدة العلوية هي: س = 6 × 6 = 36 (وحدة)

مساحة القاعدة السفلية هي: س = 12 × 12 = 144 (وحدة)

المساحة الكلية للهرم المقطوع تساوي:

صيغة حساب حجم الهرم المقطوع

وصفة:

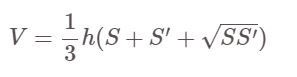
هناك:

• V: حجم الهرم المقطوع
• S، S' هي مساحات القواعد الكبيرة والصغيرة للهرم على التوالي.
• ح: ارتفاع الهرم، أي المسافة بين القاعدتين الكبيرتين والصغيرتين

هل الهرم المقطوع هو مربع (رباعي منتظم):

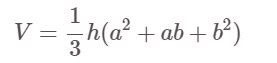
هناك:

• V: الحجم
• ح: ارتفاع الهرم
• أ، ب هما أطوال حواف القاعدة الكبيرة والقاعدة الصغيرة على التوالي.