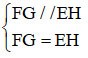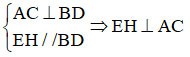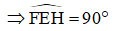كيفية حساب قطر المربع، كيفية حساب قطر المستطيل يستخدم كثيرًا في مسائل الرياضيات والتطبيقات العملية مثل التصميم والبناء، وقطع الزوايا، والقياس... قام موقع Quantrimang.com بتجميع المعرفة حول خصائص قطرين بالإضافة إلى صيغ الحساب، يرجى الرجوع إلى التطبيق في الدراسة والحياة والعمل.
جدول المحتويات
ما هو قطر المربع والمستطيل؟
قطر المربع أو المستطيل هو الخط الذي يربط بين زاويتين متقابلتين. يحتوي كل مربع ومستطيل على قطرين متساويين في الطول.
كيفية حساب قطر المربع
خصائص المربع القطري
- قطرا المربع متساويان في الطول، ومتعامدان، ويتقاطعان في منتصف كل منهما.
- هناك دائرة محصورة ودائرة محصورة ومركزا الدائرتين يتطابقان ويشكلان تقاطع قطري المربع.
- سوف يقسم قطر واحد المربع إلى مثلثين متساويي الساقين قائمين.
- يتطابق تقاطع منصفات الزوايا، والمتوسطات، والمنصفات العمودية في نقطة واحدة.
- يحتوي على جميع خصائص المستطيل والمتوازي الأضلاع والمعين.
صيغة حساب قطر المربع
وفقًا لخصائص المربع، فإن قطري المربع متساويان، وقطر واحد يقسم المربع إلى قسمين متساويين في المساحة، وهما مثلثان قائما الزاوية متساويان الساقين. وبالتالي، فإن قطر المربع هو وتر المثلثين القائمين المتساوي الساقين.
ولكي تتمكن من حساب قطر المربع، عليك فقط تطبيق نظرية فيثاغورس على المثلث القائم الزاوية.
افترض أن لديك مربع ABCD وطول ضلعه a، والقطر AC يقسم المربع إلى مثلثين قائمي الزاوية ABC وACD.
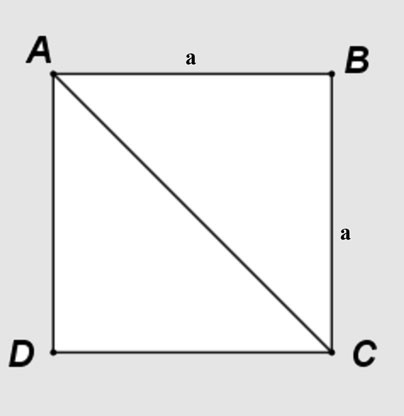
تطبيق نظرية فيثاغورس على المثلث المتساوي الساقين ABC:
⇒ ⇒
لذا فإن قطر المربع له طول ضلع يساوي:
مثال على حساب قطر المربع
مثال 1: مربع له ضلع 3 سم. قطر هذا المربع هو: 6سم، √18سم، 5سم، أو 4سم؟
حل:
أ) بتطبيق نظرية فيثاغورس في المربع ABC، لدينا:
AC² = AB² + BC² = 3² + 3² = 18
=> التيار المتردد = سم
وبالتالي فإن قطر المربع هو √18 سم.
مثال 2:
قطر المربع هو 2دسم. ضلع هذا المربع هو: 1سم، 3/2سم، √2سم أو 4/3سم؟
جائزة:
طبق نظرية فيثاغورس على المثلث القائم الزاوية ABC، لكن هذا التمرين يعطي طول القطر، أي AC = 2 سم، احسب طول الضلع AB.
لدينا: AC² = AB² + BC² = 2AB (لأن AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> أ ب = √2
كيفية حساب قطر المستطيل
المستطيل هو شكل رباعي محدب له أربع زوايا قائمة، وهو متوازي أضلاع له قطران متساويان.
خصائص أقطار المستطيل
تتمتع أقطار المستطيل بالعديد من الخصائص المهمة التي تساعد في حل المسائل التي تتضمن المستطيلات وأقطارها.
- طول قطر المستطيل هو وتر المثلث القائم الزاوية، لذا فهو يساوي الجذر التربيعي لمجموع مربعي الضلعين.
- يقسم القطر المستطيل إلى مثلثين قائمين متساويين في المساحة. وبالتالي فإن قطر المستطيل هو محور تماثل المستطيل.
- قطري المستطيل متساويان ويتقاطعان في منتصف كل خط ويشكلان 4 مثلثات متساوية الساقين.
صيغة حساب قطر المستطيل
من خصائص قطر المستطيل أعلاه، يمكننا استخدام نظرية فيثاغورس لحساب طول قطر المستطيل.
افترض أن لديك مستطيل ABCD بطول a وعرض b وقطره AC كما هو موضح أدناه.
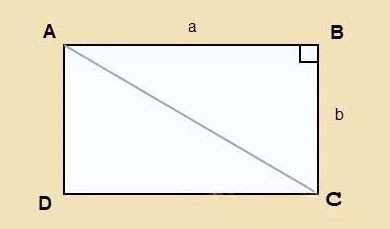
نطبق نظرية فيثاغورس على المثلث القائم ABC:
⇒ ⇒
لذلك، قطر المستطيل الذي طوله أ وعرضه ب هو:
وبالتالي فإن طول قطر المستطيل يساوي الجذر التربيعي لمجموع مربعي طولي ضلعي المستطيل (الطول والعرض).
وبالتالي، يمكننا حساب قطر المربع أو المستطيل ببساطة عن طريق تطبيق نظرية فيثاغورس.
مثال على حساب قطر المستطيل
احسب طول قطر المستطيل الذي طوله 10دسم وعرضه 5دسم.
حل:
ليكن طول قطر المستطيل a (a > 0, dm)
بتطبيق نظرية فيثاغورس فإن طول قطر المستطيل هو:
أ2 = 102 + 52 = 125
=> أ = 5√5 دسم
مثال لإثبات أن الشكل الرباعي هو مستطيل.
يمكن تطبيق خصائص وصيغة حساب قطر المستطيل لحل بعض المسائل التي تثبت أن الشكل الرباعي هو مستطيل.
إذا كان الشكل الرباعي ABCD له قطرين متعامدين على بعضهما البعض. ليكن E، F، G، H هي نقاط منتصف الأضلاع AB، BC، CD، AD على التوالي. ما هو شكل الرباعي EFGH؟ لماذا؟
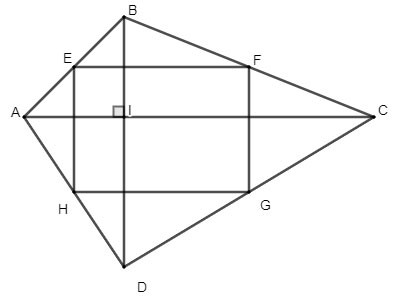
حل:
لأن E هي نقطة منتصف AB، فإن H هي نقطة منتصف AD
=> EH هو متوسط المثلث ABD.
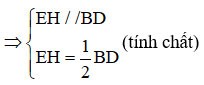 (1)
(1)
لأن F هي نقطة منتصف BC، فإن G هي نقطة منتصف CD
=> FG هو متوسط المثلث BCD
 (2)
(2)
من (1) و (2) =>
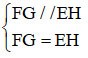
خذ بعين الاعتبار الشكل الرباعي EFGH.
FG // EH
FG = EH
=> EFGH هو متوازي أضلاع (علامة التعرف)
على الجانب الآخر:
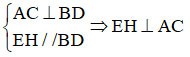
كما يحتوي أيضًا على:
E هي نقطة منتصف AB، وF هي نقطة منتصف BC.
=> EF هو متوسط المثلث ABC
=> EF // AC
لكن EH ⊥ AC => EH ⊥ EF
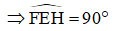
متوازي الأضلاع EFGH له زاوية قائمة
=> EFGH هو مستطيل



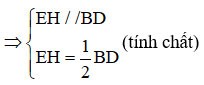 (1)
(1) (2)
(2)