صيغة حساب قطر المعين

المعين هو شكل رباعي له أربعة أضلاع متساوية، والشكل الرباعي الذي يحتوي على قطرين متعامدين على بعضهما البعض في منتصف كل خط هو معين، ومتوازي أضلاع له ضلعان متجاوران متساويان... إلى جانب المربعات والمستطيلات والمثلثات... المعين هو أحد الأشكال المهمة في الرياضيات والحياة.

بالإضافة إلى صيغة حساب محيط ومساحة المعين ، فإن طريقة حساب قطر المعين - الخط الذي يربط رؤوس المعين المتقابلة معًا - مهمة جدًا أيضًا.

ستساعدك المقالة أدناه على تعلم كيفية حساب قطر المعين بأمثلة محددة، يرجى الرجوع إليها.

جدول المحتويات

• قطر المعين
• خصائص أقطار المعين
• صيغة حساب قطر المعين
• مسألة في حساب قطر المعين

قطر المعين

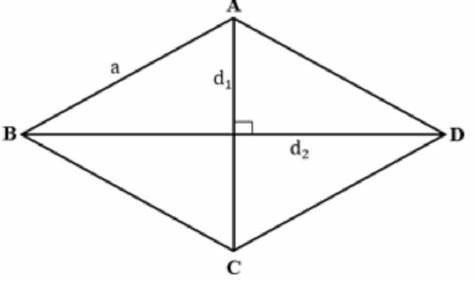
• قطر المعين هو الخط الذي يربط بين رأسين متقابلين للمعين.
• يحتوي المعين على قطرين، ويتقاطعان في منتصف المعين.
• يقسم القطر المعين إلى مثلثين متساويين الأضلاع لهما أضلاع متساوية.

خصائص أقطار المعين

يتمتع القطران في المعين بالخصائص التالية:

• قطران متساويان: قطرا المعين متساويان في الطول.
• الزاوية بين قطرين هي زاوية قائمة: يتقاطع قطرا المعين في منتصف المعين ويشكلان زاوية قائمة.
• الأقطار هي محاور تماثل المعين: كل قطر من المعين هو محور تماثل المعين، ويقسم المعين إلى نصفين متماثلين.
• الأقطار هي أقطار مثلثين متساويي الأضلاع: كل قطر من المعين هو قطر لمثلثين متساويي الأضلاع، يتكونان من ضلعين متساويين.
• حاصل ضرب طولي القطرين يساوي حاصل ضرب طولي ضلعي المعين: حاصل ضرب طولي القطرين يساوي حاصل ضرب طولي ضلعي المعين. أي أنه إذا رمزنا للقطر بـ d، وللأضلاع بـ a وb، فلدينا d² = a² + b².

هذه الخصائص هي خصائص مميزة للمعينات وتستخدم في العديد من المسائل الهندسية التي تتضمن المعينات.

صيغة حساب قطر المعين

يرجى النظر في المثال أدناه لاستنباط الصيغة لحساب قطر المعين.

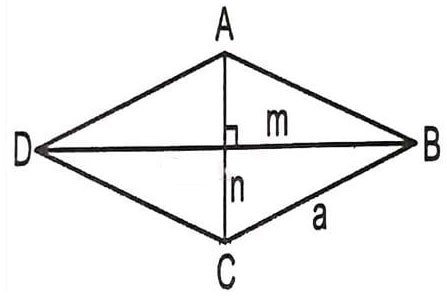
لنفترض أننا نحتاج إلى حساب طول قطر المعين ABCD مع الضلع a والزاوية ABC = 60 درجة -> ما هي الصيغة لحساب قطر المعين في هذه الحالة؟

حل:

لأن ABCD معين، فإن جميع الأضلاع متساوية.

ضع في اعتبارك المثلث ABC حيث: AB = BC = a

مرة أخرى: ABC = 60 درجة => المثلث ABC هو مثلث متساوي الأضلاع مع الضلع a.

=> AB = AC = BC = a

=> طول قطر المعين هو AC = BD = a.

الحل أعلاه هو أحد أبسط الصيغ وأسهلها فهمًا لحساب قطر المعين.

صيغة حساب قطر المعين عند معرفة المساحة والقطر المتبقي

من صيغة حساب مساحة المعين:

س = (axb) : 2

لدينا الصيغة لطول القطر على النحو التالي:

أ = س × 2 : ب

أو

ب = س × 2 : أ

هناك:

• S هي المساحة
• أ و ب هما طول القطرين

استخدم الخصائص الهندسية للمعين لحساب طول القطر دون استخدام نظرية فيثاغورس. خاصة:

قطر المعين هو متوسط ​​الارتفاعين.

القطر = الجذر التربيعي لـ (الارتفاع الطويل + الارتفاع القصير)²

قطر المعين هو نصف محيط المعين.

القطر = 1/2 × محيط المعين.

مسألة في حساب قطر المعين

المسألة 1: إذا كان لدينا معين مساحته 360 سنتيمترًا مربعًا وطول قطره 24 سنتيمترًا. احسب طول القطر الثاني

حل:

وفقًا لصيغة مساحة المعين: axb : 2

لدينا القطر الثاني: 360 × 2: 24 = 30 سم

الإجابة: 30 سم

المشكلة 2:

المعين له مساحة 4 ديسيمتر، وطول قطره الواحد هو 3/5 ديسيمتر. احسب طول القطر الثاني. حل:

طول القطر الثاني هو:

(4 × 2): 3/5 = 40/3 (دسم)

الدرس 3: قطري المعين طولهما 160 سم و 120 سم. احسب ارتفاع المعين، مع العلم أن النسبة بين الارتفاع وطول ضلع المعين هي 24:25.

حل:

مساحة المعين هي: 160.120:2 = 9600 (سم2).

وبما أن النسبة بين الارتفاع وطول ضلع المعين هي 24:25، فيمكننا اعتبار ارتفاع المعين 24a وضلع المعين 25a.

ثم لدينا مساحة المعين: 25 أ. 24 أ = 9600 أ2 = 16 أ = 4 سم.

ارتفاع المعين هو: 24.4 = 96 (سم).

وبالتالي فإن ارتفاع المعين هو 96 سم.

الدرس الرابع: 

إذا كان المعين ABCD له طول ضلع 12.5 سم وارتفاع 6.72 سم و AC أصغر من BD. ما هو طول القطرين AC وBD على التوالي؟

جائزة:

استخدم الصيغة لحساب مساحة المعين: S = ha = 6.72 × 12.5 = 84 سم.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

ليكن O هو تقاطع قطري المعين.

لدينا AOB هو مثلث قائم الزاوية عند O لذا AB2 = OA2 + OB2

حيث، OA = 1/2 AC، OB = 1/2 BD

=> 12.52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (وفقًا للمشكلة BD > AC) (2)

من (1) و (2)، لدينا:

BD = 24، AC = 7 سم.

الدرس الخامس: 

المعين ABCD له أضلاع تساوي 10 وحدات. احسب طول قطر المعين.

الحل: طول قطر المعين ABCD هو:

القطر = الجذر التربيعي لـ 2(10²) = الجذر التربيعي لـ 200 = 14.14 وحدة طول.

وبالتالي فإن طول قطر المعين ABCD يساوي 14.14 وحدة طول.

الدرس السادس:

المعين ABCD يحتوي على قطر مكون من 12 وحدة. احسب محيط المعين.

الحل: بما أن المعين له أربعة أضلاع متساوية، فإن محيطه سيكون مجموع أطوال الأضلاع الأربعة، أي:

المحيط = 4 × طول الضلع = 4 × 6 = 24 وحدة طول.

وبالتالي فإن محيط المعين ABCD هو 24 وحدة طول.