صيغة حساب مساحة السطح وحجم الكرة

دعونا نتعلم ونراجع صيغة حساب مساحة السطح وحجم الكرة مع Quantrimang.com في المقال أدناه.

جدول المحتويات

• ما هي الكرة؟
  • ما هي الكرة؟
• صيغة حساب مساحة السطح وحجم الكرة
  • صيغة حساب مساحة سطح الكرة
  • صيغة حساب حجم الكرة:
• صيغة حساب نصف قطر الكرة
  • الكرة المحيطة بالهرم لها ضلع عمودي على القاعدة.
  • رباعي السطوح المربع (هذه حالة خاصة من الصيغة 1)
  • المنشور الرأسي له قاعدة عبارة عن مضلع محفور.
  • صيغة رباعي السطوح الذي رؤوسه هي رؤوس منشور قائم
  • صيغة حساب نصف قطر الكرة للهرم ذي الوجوه الجانبية العمودية على القاعدة
• أمثلة على حساب مساحة السطح وحجم الكرة

ما هي الكرة؟

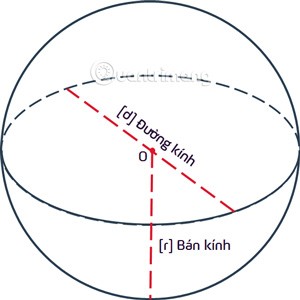
الكرة هي موضع النقاط المتساوية البعد عن نقطة ثابتة معينة O rفي الفضاء ثلاثي الأبعاد. تسمى النقطة O بالمركز والمسافة rتسمى بنصف قطر الكرة.

ما هي الكرة؟

الكرة هي مجموعة من النقاط التي تقع داخل كرة وتسمى الكرة كرة أو كرة مركزها O ونصف قطرها r = OA.

صيغة حساب مساحة السطح وحجم الكرة

صيغة حساب مساحة سطح الكرة

مساحة سطح الكرة هي أربعة أضعاف مساحة الدائرة الكبيرة، أي أربعة أضعاف الثابت باي مضروبًا في مربع نصف قطر الكرة.

صيغة حساب حجم الكرة:

يتم حساب حجم الكرة، المعروف أيضًا باسم حجم الكرة، عن طريق ضرب ثلاثة أرباع باي في مكعب نصف قطر الكرة.

هناك:

• Sهي مساحة سطح الكرة
• Vهو حجم الكرة
• rهو نصف قطر الكرة/الكرة
• dهي كرة/كرة

صيغة حساب نصف قطر الكرة

الكرة المحيطة بالهرم لها ضلع عمودي على القاعدة.

• Rd هو نصف قطر القاعدة.
• h هو طول الضلع العمودي على القاعدة.

على سبيل المثال : إذا أعطينا هرمًا S.ABCD بقاعدة مستطيلة حيث AB = 3a، BC = 4a، SA = 12a وSA عمودي على القاعدة. احسب نصف قطر R للكرة المحيطة بالهرم S.ABCD.

الحل: لدينا

لذا

رباعي السطوح المربع (هذه حالة خاصة من الصيغة 1)

تحتوي الكتلة المربعة OABC على OA وOB وOC، وهي متعامدة على بعضها البعض ولها:

على سبيل المثال:

يحتوي رباعي السطوح OABC على OA وOB وOC، متعامدين بشكل متبادل، وله نصف قطر كرة محدد يبلغ . أكبر حجم للرباعي السطوح OABC

الحل : لدينا

ومن ناحية أخرى لدينا:

وفقًا لعدم المساواة بين AM وGM، لدينا:

المنشور الرأسي له قاعدة عبارة عن مضلع محفور.

هناك:

• Rd هو نصف قطر القاعدة
• h هو طول الضلع.

مثال 1: إذا أعطينا كرة نصف قطرها R تحيط بمكعب طول ضلعه a. أي من العبارات التالية صحيحة؟

أ.

ب.

ج.

د.

الحل: لدينا

إذن الجواب هو ج.

صيغة رباعي السطوح الذي رؤوسه هي رؤوس منشور قائم

يحتوي الشكل الرباعي (H1) على رؤوس هي رؤوس المنشور الرأسي (H2)، إذن:

صيغة حساب نصف قطر الكرة للهرم ذي الوجوه الجانبية العمودية على القاعدة

حيث R، d هو نصف قطر القاعدة؛ أ، س هما على التوالي طول تقاطع الوجه الجانبي والقاعدة، والزاوية في الجزء العلوي من الوجه الجانبي المطل على القاعدة.

أو يمكنك استخدام الصيغة

حيث: Rb هو نصف القطر المحيط بالوجه الجانبي وa هو طول تقاطع الوجه الجانبي مع القاعدة.

على سبيل المثال: 

إذا كان لدينا هرم S.ABCD ذو قاعدة مربعة، ومثلث متساوي الأضلاع SAD، وضلعه √2a، ويقع في مستوى عمودي على القاعدة. احسب نصف قطر R للكرة المحيطة بالهرم S.ABCD.

أ.

ب.

الحل: لدينا

الإجابة الصحيحة هي ب.

أمثلة على حساب مساحة السطح وحجم الكرة

الدرس الأول : إذا كانت لدينا دائرة محيطها 31.4 سم. احسب حجم الكرة التي نصف قطرها يساوي نصف قطر الدائرة المعطاة.

جائزة:

محيط الدائرة C = 2πr = 31.4 سم

=> نصف القطر r = C/2π = 5 سم

حجم الكرة المعطاة هو:

V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523.3 سم³

الدرس 2 : احسب حجم الكرة التي قطرها d = 4 سم.

جائزة:

نصف القطر r = d/2 = 2 سم

حجم الكرة هو:

V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33.49 سم³

الدرس الثالث :

دع دائرة قطرها 4أ تدور حول قطرها. ما هو حجم الجسم الصلب الدوار إذن؟

الحل: إذا كانت لدينا دائرة قطرها 4a تدور حول قطرها، نحصل على كرة قطرها 4a أو نصف قطرها R = 2a.

حجم الكرة هو:

الدرس الرابع :

الكرة التي نصف قطرها R√3 لها مساحة:

أ. 4√3πR2

ب. 4πR2

ج. 6πR2

د. 12πR2

الحل: طبق الصيغة: S = 4πR2

مساحة سطح كرة نصف قطرها R√3 هي: S = 4π(R√3)2 = 12πR2

الجواب إذن هو د.

صيغتان قصيرتان ولكن تذكرهما لفترة طويلة أمر صعب للغاية. قم بوضع إشارة مرجعية على المقالة وافتحها عندما تحتاج إليها. آمل أن تكون هذه المقالة مفيدة لك.

بالإضافة إلى صيغة حساب مساحة السطح وحجم الكرة أعلاه، يمكنك أيضًا الرجوع إلى صيغة حساب مساحة بعض الأشكال الأساسية الأخرى مثل المثلثات والمستطيلات ومتوازي الأضلاع . ..