صيغة حساب مساحة المثلث: قائم، منتظم، متساوي الساقين، متساوي الأضلاع

ما هي صيغة حساب مساحة المثلث المنتظم القائم المتساوي الساقين ؟ يرجى الرجوع إلى المقال أدناه لفهم أسهل الطرق وأكثرها استخدامًا لحساب مساحة المثلث.

جدول المحتويات

• 1. احسب مساحة المثلث المنتظم
• 2. احسب مساحة المثلث المتساوي الساقين
• 3. احسب مساحة المثلث المتساوي الأضلاع
• 4. احسب مساحة المثلث القائم
• 5. احسب مساحة المثلث المتساوي الساقين القائم
• 6. صيغة حساب مساحة المثلث في نظام إحداثيات أوكسي زد
• أنواع المثلثات

1. احسب مساحة المثلث المنتظم

المثلث ABC له ثلاثة أضلاع a، b، c، ha هو الارتفاع من الرأس A كما هو موضح:

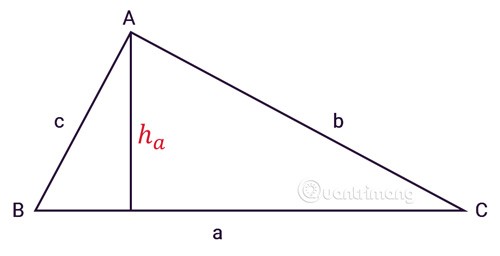
أ. الصيغة العامة

مساحة المثلث تساوي الارتفاع مضروبًا في طول الضلع المقابل (القاعدة) ومقسومًا على 2.

قصيدة عن حساب مساحة المثلث المنتظم

مساحة المثلث سهلة.
اضرب الارتفاع في القاعدة ثم قسمه إلى نصفين.

على سبيل المثال:

احسب مساحة مثلث طول قاعدته 5م وارتفاعه 24دسم.

الحل: الارتفاع 24 دسم ​​= 2.4 متر

مساحة المثلث هي:

ب. احسب مساحة المثلث عندما تكون إحدى زواياه معروفة

مساحة المثلث تساوي نصف حاصل ضرب طولي ضلعين متجاورين في جيب الزاوية المحصورة بين هذين الضلعين في المثلث.

على سبيل المثال:

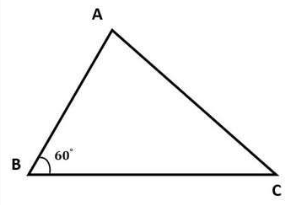
المثلث ABC له ضلع BC = 7، وضلع AB = 5، والزاوية B تساوي 60 درجة. احسب مساحة المثلث ABC ؟

جائزة:

ج. احسب مساحة المثلث عند معرفة أضلاعه الثلاثة باستخدام صيغة هيرون.

باستخدام صيغة هيرون المجربة:

مع كون p هو نصف محيط المثلث:

يمكن إعادة كتابتها باستخدام الصيغة:

على سبيل المثال:

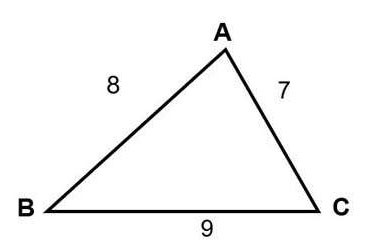
احسب مساحة المثلث الذي أطوال أضلاعه AB = 8، AC = 7، CB = 9

جائزة:

نصف محيط المثلث ABC هو

بتطبيق صيغة البطل لدينا

د. احسب المساحة بنصف قطر الدائرة المحيطة بالمثلث (R).

آخر:

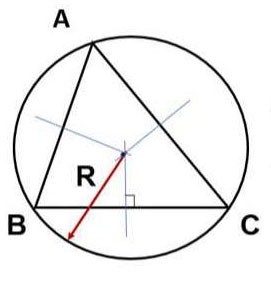
ملحوظة: من الضروري إثبات أن R هو نصف قطر الدائرة المحيطة بالمثلث.

على سبيل المثال:

إذا كان لدينا مثلث ABC، فإن أطوال الأضلاع هي a = 6، b = 7، c = 5، R = 3 (R هو نصف قطر الدائرة المحيطة بالمثلث ABC). احسب مساحة المثلث ABC

جائزة:

هـ. احسب المساحة باستخدام نصف قطر الدائرة المحيطة بالمثلث (r).

• ص: نصف محيط المثلث.
• ر: نصف قطر الدائرة المحفورة.

على سبيل المثال: احسب مساحة المثلث ABC مع العلم أن أطوال الأضلاع AB = 20، AC = 21، BC = 15، r = 5 (r هو نصف قطر الدائرة المحيطة بالمثلث ABC).

جائزة:

نصف محيط المثلث هو:

ر= 5

مساحة المثلث هي:

2. احسب مساحة المثلث المتساوي الساقين

المثلثات متساوية الساقين تشبه المثلثات المنتظمة، ويمكننا تطبيق صيغة ضرب الارتفاع في القاعدة، ثم القسمة على 2 كما هو موضح أعلاه. ستكون هناك أيضًا صيغ متقدمة أكثر تعقيدًا:

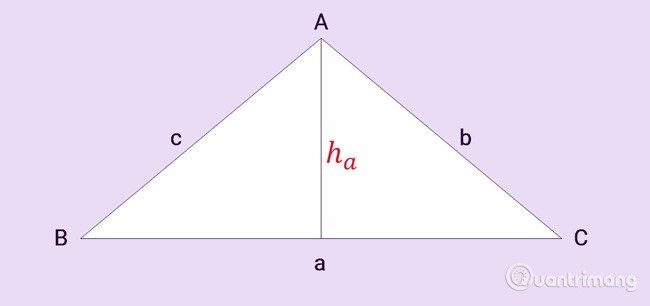
المثلث متساوي الساقين ABC له ثلاثة أضلاع، a هو طول القاعدة، b هو طول الضلعين، ha هو الارتفاع من الرأس A كما هو موضح:

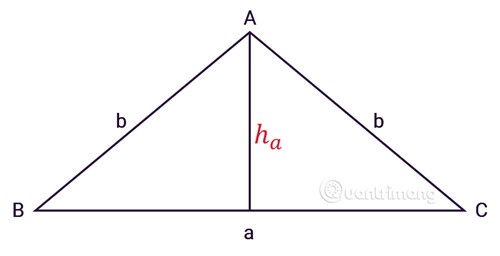
بتطبيق صيغة حساب مساحة المثلث المنتظم، نحصل على صيغة حساب مساحة المثلث المتساوي الساقين:

3. احسب مساحة المثلث المتساوي الأضلاع

المثلث المتساوي الأضلاع ABC له ثلاثة أضلاع متساوية، a هو طول الأضلاع كما هو موضح:

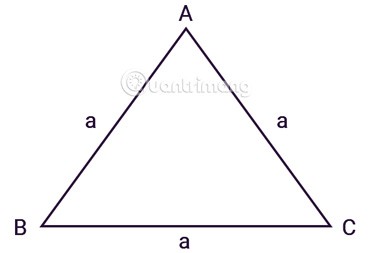
بتطبيق نظرية هيرون للاستنتاج، لدينا الصيغة لحساب مساحة المثلث المتساوي الأضلاع:

4. احسب مساحة المثلث القائم

المثلث ABC قائم الزاوية في B، a، b هما طولا الضلعين القائمي الزاوية:

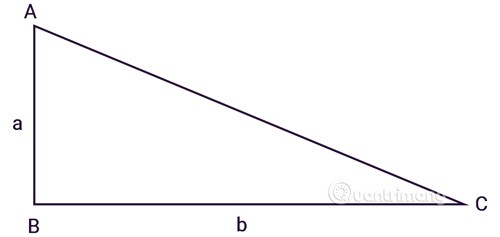
طبق صيغة حساب مساحة المثلث القائم بحيث يكون الارتفاع هو أحد الضلعين القائمين والقاعدة هي الضلع المتبقي.

صيغة حساب مساحة المثلث القائم:

قصيدة عن حساب مساحة المثلث القائم:

مثلث ذو زاويتين قائمتين.
حافظ على هدوئك، لا داعي للذعر ولا ترتكب الأخطاء.

الجانب، الجانب مضروبًا في، مقسومًا على اثنين
هي المساحة، قم بالتمرين بسرعة

5. احسب مساحة المثلث المتساوي الساقين القائم

المثلث ABC هو مثلث قائم الزاوية في A، a هو طول الضلعين:

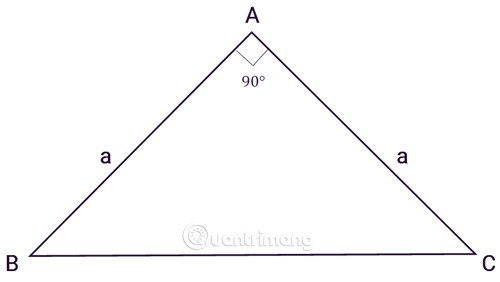
بتطبيق صيغة حساب مساحة المثلث القائم على مساحة المثلث القائم متساوي الساقين ذو الارتفاع والقاعدة المتساوية، نحصل على الصيغة:

6. صيغة حساب مساحة المثلث في نظام إحداثيات أوكسي زد

من الناحية النظرية، يمكننا استخدام الصيغ أعلاه لحساب مساحة المثلث في الفضاء أو في فضاء أوكسييز. ومع ذلك، فإن هذا سوف يسبب بعض الصعوبة في الحساب. لذلك، في فضاء أوكسي، يحسب الناس في كثير من الأحيان مساحة المثلث باستخدام المنتج الاتجاهي.

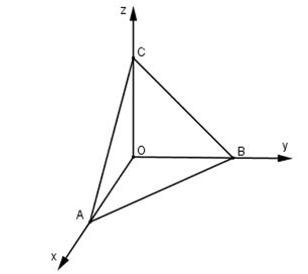
في الفضاء أوكسي زد، المثلث ABC معطى. يتم حساب مساحة المثلث ABC بالصيغة التالية:

مثال :

في فضاء أوكسي، المثلث ABC المعطى مع إحداثيات ثلاث رؤوس A(-1؛1؛2)، B(1؛2؛3)، C(3؛-2؛0). احسب مساحة المثلث ABC

حل :

لدينا:

لحساب مساحة المثلث، عليك تحديد نوع المثلث، ومن ثم إيجاد صيغة حساب المساحة الصحيحة والعوامل اللازمة لحساب مساحة المثلث في أسرع وقت ممكن.

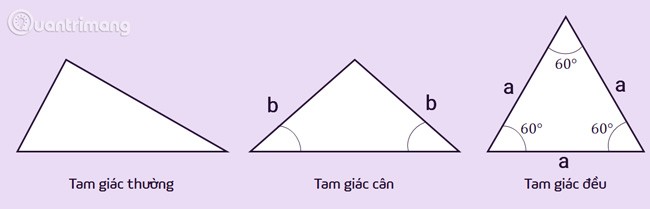
أنواع المثلثات

المثلث المنتظم: هو المثلث الأساسي، وله أطوال أضلاع مختلفة، وقياسات زوايا داخلية مختلفة. يمكن أن تشمل المثلثات المنتظمة أيضًا حالات خاصة من المثلثات.

المثلث المتساوي الساقين: هو مثلث له ضلعان متساويان، ويسمى هذان الضلعان بالضلعين الجانبيين. رأس المثلث المتساوي الساقين هو تقاطع ضلعين متجاورين. الزاوية التي تشكلها الرأس تسمى زاوية الرأس، والزاويتان الأخريان تسمى زاويتي القاعدة. خاصية المثلث المتساوي الساقين هي أن الزاويتين في القاعدة متساويتان.

المثلث المتساوي الأضلاع: هو حالة خاصة من المثلث المتساوي الساقين حيث تكون جميع أضلاعه الثلاثة متساوية. خاصية المثلث المتساوي الأضلاع هي أن له 3 زوايا متساوية وقياسها 60 درجة.

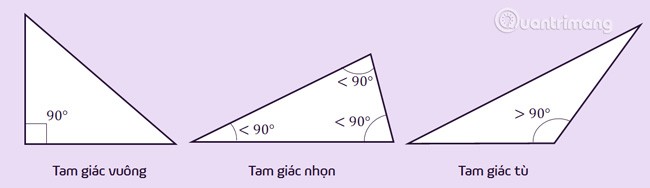
المثلث القائم: هو مثلث تكون إحدى زواياه تساوي 90 درجة (زاوية قائمة).

المثلث المنفرج: هو مثلث تكون زاوية داخلية فيه أكبر من 90 درجة (زاوية منفرجة) أو زاوية خارجية فيه أقل من 90 درجة (زاوية حادة).

المثلث الحاد: هو مثلث به ثلاث زوايا داخلية، جميعها أقل من 90 درجة (ثلاث زوايا حادة) أو به جميع زواياه الخارجية أكبر من 90 درجة (ست زوايا منفرجة).

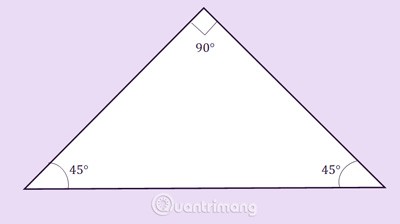
المثلث القائم المتساوي الساقين: هو مثلث قائم ومثلث متساوي الساقين.

• صيغة حساب محيط المثلث
• صيغة حساب الارتفاع في المثلث المنتظم، والمتساوي الساقين، والمتساوي الأضلاع، والمثلث القائم الزاوية
• ما هو التركيز؟ صيغة حساب مركز ثقل المثلث
• ما هو المنصف العمودي؟

ما سبق هو ملخص لصيغ حساب مساحة المثلث الشائعة، وحساب مساحة المثلث في نظام إحداثيات oxyz. إذا كان لديك أي مخاوف أو أسئلة أو مساهمات، يرجى ترك تعليق أدناه لمناقشتها مع Quantrimang.com.