تعتبر صيغة حساب مساحة ومحيط متوازي الأضلاع من المعلومات الأساسية. يرجى الرجوع إلى الصيغة التي قام موقع Quantrimang.com بتجميعها أدناه.
جدول المحتويات
1. مساحة متوازي الأضلاع
يتم قياس مساحة متوازي الأضلاع بحجم مساحة السطح، وهو الجزء المسطح المرئي من متوازي الأضلاع.
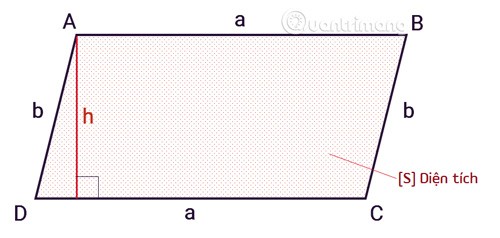
يتم حساب مساحة متوازي الأضلاع بالصيغة التي تساوي حاصل ضرب القاعدة في الارتفاع.
SABCD = axh
هناك:
Sهي مساحة متوازي الأضلاع.aهي قاعدة متوازي الأضلاع.hهو الارتفاع من الأعلى إلى القاعدة لمتوازي الأضلاع.
2. محيط متوازي الأضلاع
يتم حساب محيط متوازي الأضلاع عن طريق إضافة طول الخطوط المحيطة بالشكل، وهو أيضًا الخط المحيط بالمنطقة بأكملها، أي ما يعادل 2 مرات مجموع أي زوج من الأضلاع المتجاورة.
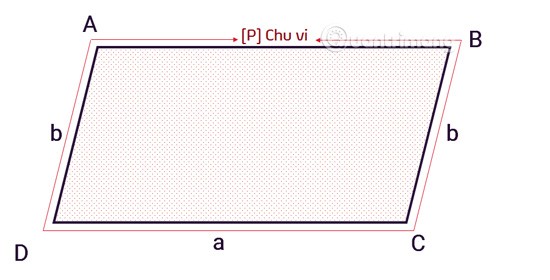
بمعنى آخر، محيط متوازي الأضلاع هو مجموع أطوال الأضلاع الأربعة. الصيغة المحددة هي كما يلي:
ج = 2 × (أ + ب)
هناك:
Cهو محيط متوازي الأضلاع.aوهما bضلعان متجاوران في متوازي الأضلاع.
3. ما هو متوازي الأضلاع؟
يُعرِّف
متوازي الأضلاع هو شكل رباعي الأضلاع يحتوي على زوجين من الأضلاع المتوازية أو زوج واحد من الأضلاع المتوازية والمتساوية. يحتوي متوازي الأضلاع على زاويتين متقابلتين ومتساويتين وقطرين يتقاطعان في منتصف الشكل.
يمكن اعتبار متوازي الأضلاع حالة خاصة من شبه المنحرف.
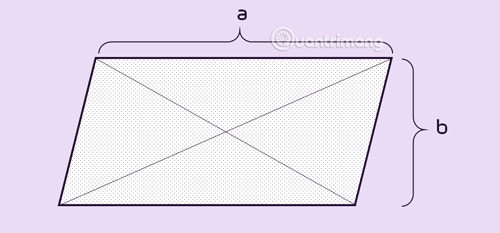
خصائص متوازي الأضلاع
في متوازي الأضلاع:
- الأضلاع المتقابلة متساوية.
- الزوايا المتقابلة متساوية.
- يتقاطع قطريان في منتصف كل خط.
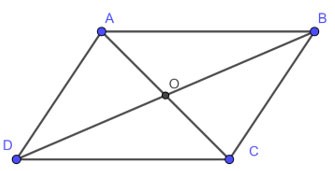
ABCD هو متوازي أضلاع، AC يتقاطع مع BD في O. ثم:
• AB = CD، AD = BC
•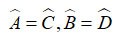
• OA = OC، OB = OD
علامات التعرف
أ) الشكل الرباعي الذي فيه ضلعان متقابلان متوازيان هو متوازي أضلاع.
ب) الشكل الرباعي الذي فيه ضلعان متقابلان متساويان هو متوازي أضلاع.
ج) الشكل الرباعي الذي فيه ضلعان متقابلان متوازيان ومتساويان هو متوازي أضلاع.
د) الشكل الرباعي الذي فيه زاويتان متقابلتان ومتساويتان هو متوازي أضلاع.
هـ) الشكل الرباعي الذي يتقاطع فيه قطران في منتصف كل منهما هو متوازي أضلاع.
4. أسئلة اختيارية متعددة لمراجعة متوازيات الأضلاع
التمرين 1 : اختر الجملة الخاطئة.
أ. متوازي الأضلاع له قطران يتقاطعان في منتصف كل قطر.
ب. متوازي الأضلاع له زاويتان متقابلتان متساويتان
ج. متوازي الأضلاع له قطران متعامدان على بعضهما البعض.
د. متوازيا الأضلاع لهما زوجان من الأضلاع المتقابلة المتوازية.
حل
في متوازي الأضلاع:
+ متوازي الأضلاع له ضلعان متقابلان متوازيان
+ الأضلاع المتقابلة متساوية
+ يتقاطع قطريان في منتصف كل خط، لذا فإن C غير صحيح.
الإجابة الصحيحة هي: ج
التمرين 2 : متوازي الأضلاع ABCD معطى حيث Â = α > 900. خارج متوازي الأضلاع، ارسم مثلثين متساويي الأضلاع ADE وABF. ما هو نوع المثلث CEF؟ اختر أفضل إجابة
أ. المثلث
ب. مثلث متساوي الساقين
ج. مثلث متساوي الأضلاع
د. مثلث منفرج الزاوية
إجابة:
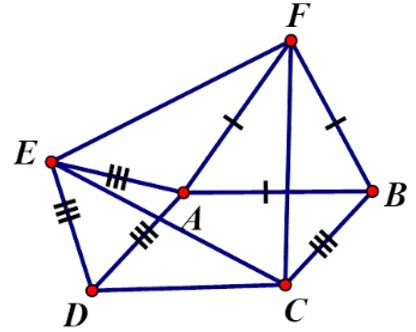

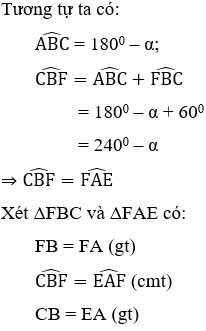
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
من (1) و (2) يمكننا أن نستنتج أن CF = FE = EC، وبالتالي فإن المثلث CEF متساوي الأضلاع.
الدرس 3 : اختر الجملة الخاطئة ABCD هو متوازي أضلاع. ثم:
أ. أ ب = د ج
ب. ميلادي = قبل الميلاد
ج. اختبار متوازي الأضلاع مع الإجابات
د. AC = BD
حل
في متوازي الأضلاع:
+ متوازي الأضلاع له ضلعان متقابلان متوازيان
+ الأضلاع المتقابلة متساوية
+ يتقاطع قطريان في منتصف كل خط، لذا فإن D غير صحيح.
الدرس 4 : املأ الفراغ بالعبارة المناسبة: "الشكل الرباعي الذي يحتوي على قطرين... هو متوازي أضلاع".
أ. متساوي
ب. تتقاطع
ج. تتقاطع في منتصف كل خط
د. متوازي
حل
العلامات:
الشكل الرباعي الذي يتقاطع فيه قطران في منتصف كل منهما هو متوازي أضلاع.
الدرس 5 : اختر الجملة الخاطئة:
أ. الشكل الرباعي الذي يحتوي على زوجين من الأضلاع المتقابلة المتوازية هو متوازي أضلاع.
ب. شبه المنحرف الذي له زاويتان متساويتان متجاورتان لقاعدة هو متوازي أضلاع.
ج. الشكل الرباعي الذي يحتوي على زوجين من الأضلاع المتقابلة المتساوية هو متوازي أضلاع.
د. الشكل الرباعي الذي فيه زوجان من الزوايا المتقابلة المتساوية هو متوازي أضلاع.
حل
العلامات:
+ الشكل الرباعي الذي له ضلعان متقابلان متوازيان هو متوازي أضلاع لذا فإن A صحيحة.
+ الشكل الرباعي الذي له ضلعان متقابلان متساويان هو متوازي أضلاع لذا فإن D صحيحة.
+ الشكل الرباعي الذي به زاويتان متقابلتان ومتساويتان هو متوازي أضلاع لذا فإن D صحيحة.
بإدراك أن شبه المنحرف الذي له زاويتان متساويتان متجاورتان لقاعدة هو شبه منحرف متساوي الساقين، لذا فإن B غير صحيح.
الإجابة الصحيحة هي: ب
5. أمثلة على حساب محيط ومساحة متوازي الأضلاع
مثال 1 : إذا كان لدينا متوازي أضلاع طول قاعدته 12 سم، وطول ضلعه 7 سم، وارتفاعه 5 سم. احسب محيط ومساحة هذا المتوازي الأضلاع؟
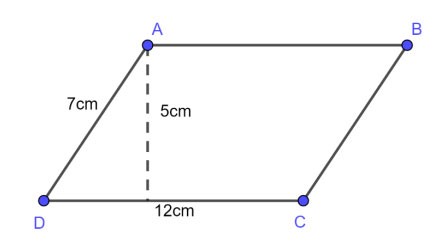
جائزة:
محيط متوازي الأضلاع هو:
ص = 2 × (12 + 7) = 38 (سم)
مساحة متوازي الأضلاع هي:
S = axh = 12 × 5 = 60 (سم2)
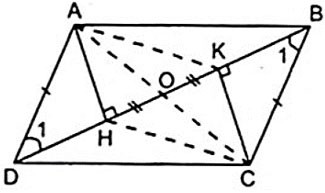
مثال 2:
معطى متوازي الأضلاع ABCD حيث H وK هما أقدام الارتفاعات المرسومة من الرؤوس A وC إلى BD على التوالي.
أ) أثبت أن AHCK هو متوازي أضلاع.
ب) ليكن O هو منتصف HK. أثبت أن A، O، C متوازيان.
التعليمات:
أ) من الفرضية لدينا:
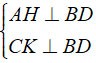 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 )
بتطبيق خصائص أضلاع متوازي الأضلاع وخصائص الزوايا المتبادلة، لدينا:
 ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK
(الوتر - حالة الزاوية الحادة)
⇒ AH = CK (الأضلاع المتقابلة متساوية) (2)
من (1) و (2) لدينا شكل رباعي AHCK ذو ضلعين متقابلين متوازيين ومتساويين وهو متوازي أضلاع.
ب) تطبيق خصائص أقطار متوازي الأضلاع AHCK
يحتوي متوازي الأضلاع AHCK على قطريين AC و HK يتقاطعان في نقطة منتصف كل خط. نظرًا لأن O هي نقطة المنتصف لـ HK، فإن O هي أيضًا نقطة المنتصف لـ AC.
⇒ A، O، C على خط مستقيم.
بالإضافة إلى متوازيات الأضلاع، فإن صيغ حساب مساحة ومحيط الأشكال الهندسية الأخرى الشائعة مثل المعينات ، والمربعات ، وشبه المنحرفات ، والمستطيلات ... هي أيضًا مهمة جدًا وتطبق على نطاق واسع في الدراسة والحياة.
نأمل من خلال المقالة أعلاه أن تكون قد فهمت واستوعبت المعرفة الأساسية حول متوازيات الأضلاع بشكل أفضل. يرجى ترك تعليق أدناه إذا كان لديك أي أسئلة أو تعليقات لمناقشتها مع Quantrimang.com.



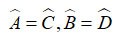



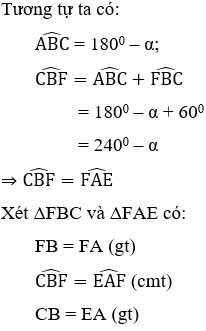


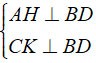 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 ) ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK










