دعونا نتعرف على صيغة حساب المساحة الجانبية والمساحة الكلية وارتفاع الأسطوانة لتطبيقها في الدراسة والحياة اليومية.
جدول المحتويات
كيفية حساب مساحة الاسطوانة
تتضمن مساحة الأسطوانة المساحة الجانبية والمساحة الكلية.
يمكنك إدخال ارتفاع ونصف قطر الأسطوانة في الجدول أدناه لمعرفة المساحة الجانبية والمساحة الكلية للأسطوانة.
صيغة حساب المساحة الجانبية للاسطوانة
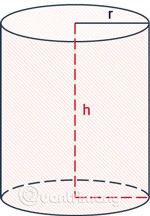
تتضمن المساحة الجانبية للأسطوانة فقط مساحة السطح المحيط بالأسطوانة، ولا تشمل مساحة القاعدتين.
صيغة حساب المساحة الجانبية للأسطوانة هي محيط دائرة القاعدة مضروبًا في الارتفاع.
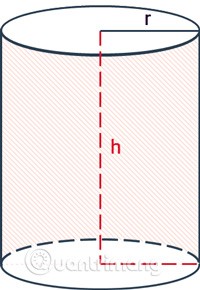 |
هناك:
- المنطقة المحيطة هي المنطقة المحيطة.
rهو نصف قطر الاسطوانة.hهو الارتفاع، المسافة بين قاعدتي الأسطوانة.
|
مثال: 1
أسطوانة دائرية لها نصف قطر القاعدة r = 5 سم، والارتفاع h = 7 سم. احسب المساحة الجانبية للاسطوانة الرأسية
الحل: مساحة سطح الأسطوانة الدائرية: Sxq = 2.π.rh = 2π.5.7 = 70π = 219.8 (سم2).
مثال: 2
معطى المربع ABCD مع الضلع 2a. ليكن O و O' نقطتي منتصف الضلعين AB و CD على التوالي. عندما نقوم بتدوير هذا المربع حول المحور OO، نحصل على أسطوانة دوارة. احسب مساحة سطح الاسطوانة الدوارة
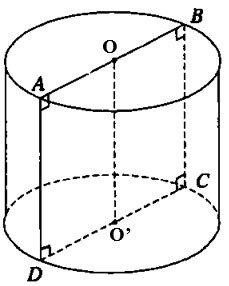
حل:
نصف قطر الدائرة القاعدية هو r= CD= a
ارتفاع الاسطوانة هو h= OO'= AD=2a
إذن المساحة الجانبية للأسطوانة هي Sxq = 2πrh = 2π.a.2a =4a2π
صيغة حساب المساحة الكلية للاسطوانة
يتم حساب المساحة الكلية على أنها مقدار المساحة الكلية التي يشغلها الشكل، بما في ذلك المساحة الجانبية ومساحة القاعدتين الدائريتين.
صيغة حساب المساحة الكلية للأسطوانة هي المساحة الجانبية بالإضافة إلى مساحة القاعدتين.
مثال 1 : احسب المساحة الكلية لأسطوانة قاعدتها 3 وارتفاعها 5.
حل:
المساحة الكلية هي Stp = Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
احسب ارتفاع الاسطوانة
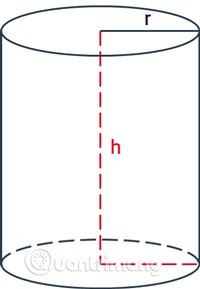
ارتفاع الأسطوانة هو المسافة بين قاعدتي الأسطوانة.
حساب ارتفاع الأسطوانة عند معرفة المساحة الكلية ونصف قطر القاعدة
على سبيل المثال: إذا كان لدينا أسطوانة ذات نصف قطر قاعدة R = 8 سم ومساحة إجمالية 564π سم2. احسب ارتفاع الاسطوانة.
جائزة:
لدينا
حساب ارتفاع الاسطوانة عند معرفة المساحة الجانبية
=>
صيغة حساب نصف قطر قاعدة الأسطوانة
1. صيغة حساب محيط الدائرة؛ مساحة الدائرة
الدائرة محيطها C=2πr
=>
الدائرة ذات القاعدة لها مساحة S=πr2
=>
على سبيل المثال. احسب نصف قطر قاعدة الأسطوانة في الحالات التالية:
أ. محيط الدائرة القاعدية هو 6π
ب. مساحة القاعدة هي 25π
حل:
أ. نصف قطر الدائرة القاعدية هو
ب. نصف قطر الدائرة القاعدية هو
2. القاعدة هي الدائرة المرسومة في المضلع
- محصور في أي مثلث: حيث S هي مساحة المثلث و p هو نصف المحيط
- محصور في مثلث متساوي الأضلاع: الضلع
- المربع المنقوش:
مثال 1 . معطى أسطوانة محفورة داخل مكعب ضلعه أ. احسب نصف قطر تلك الأسطوانة.
نصف قطر الاسطوانة هو:
مثال 2 . بالنظر إلى المنشور المنتظم ABC.A'B'C' مع ، الحجم المحيط بالأسطوانة. احسب نصف قطر تلك الأسطوانة.
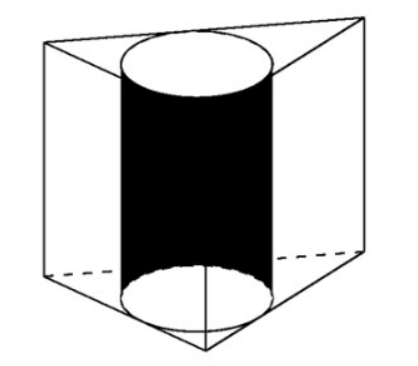
حجم المنشور هو
قاعدة المنشور المنتظم هي مثلث متساوي الأضلاع، لذا => الضلع
وبالتالي فإن نصف قطر قاعدة الأسطوانة هو:
3. القاعدة هي الدائرة التي تحيط بالمضلع.
مُحاط بأي مثلث:
هناك:
- أ، ب، ج هي أطوال الأضلاع الثلاثة للمثلث
- p هو نصف محيط المثلث:
محيط المثلث القائم: الوتر
محيط المثلث المتساوي الأضلاع: الضلع
محيط المربع: الضلع
على سبيل المثال:
احسب نصف قطر قاعدة الأسطوانة المحيطة بالهرم المنتظم S.ABC في الحالات التالية:
أ. ABC هو مثلث قائم الزاوية عند A حيث AB = a و AC = a√3
ب. ABC لديه AB = 5؛ التيار المتردد= 7؛ ق م=8
جائزة:
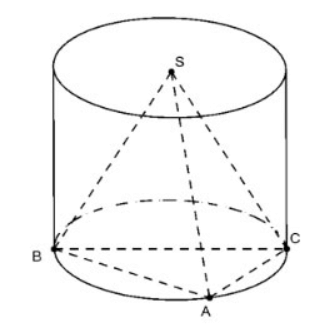
أ. وتر الزاوية الداخلية
لأن ABC زاوية قائمة عند A، نصف القطر R=0.5.BC=a
ب. نصف محيط المثلث ABC هو
ما هي الاسطوانة الدائرية؟
الأسطوانة الدائرية هي أسطوانة لها قاعدتان دائريتان متساويتان ومتوازيتان مع بعضهما البعض.
تُستخدم الأسطوانات بشكل شائع جدًا في مسائل الهندسة من الأساسية إلى المعقدة، حيث تُستخدم صيغة حساب مساحة وحجم الأسطوانات غالبًا بشكل مختلف. إذا كنت تعرف بالفعل كيفية حساب مساحة ومحيط الدائرة، فيمكنك بسهولة استنتاج الصيغ لحساب الحجم والمساحة الجانبية والمساحة الكلية للأسطوانة.
صيغة حساب مساحة المقطع العرضي للاسطوانة
قطع الأسطوانة بالطائرة (P) من خلال المحور
- والمقطع العرضي الناتج هو عبارة عن مستطيل.
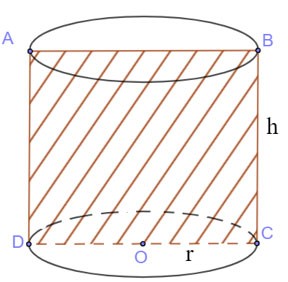 |
مساحة المقطع العرضي:
SABCD = BC.CD = 2r.h
|
قطع الأسطوانة بالمستوى (P) الموازي للمحور وعلى مسافة x منه
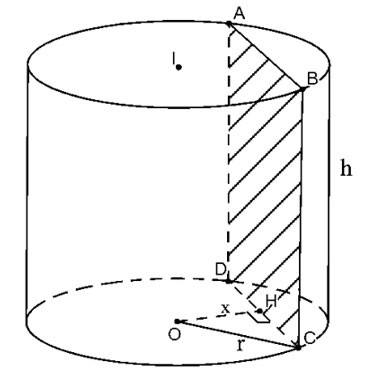 |
المقطع العرضي الناتج هو المستطيل ABCD كما هو موضح أعلاه.
ليكن H هو نقطة المنتصف لـ CD، لدينا OH ⊥ CD=>
لذلك فإن مساحة المقطع العرضي
|
قطع الأسطوانة بالمستوى (P) غير العمودي على المحور ولكن قطع جميع مولدات الأسطوانة
 |
المقطع العرضي المتكون عبارة عن دائرة مركزها O' ونصف قطرها O'A'=r
مساحة المقطع العرضي: S= πr2
|
قم بقطع الأسطوانة بالمستوى (P) غير العمودي على المحور ولكن قم بقطع جميع مولدات الأسطوانة.
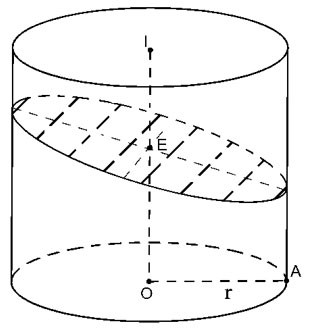 |
المقطع العرضي الناتج هو شكل بيضاوي (E) مع محور ثانوي 2r => a=r
المحور الكبير يساوي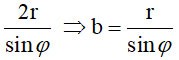
مع 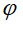 الزاوية بين محور OI و (P) الزاوية بين محور OI و (P)
لذلك المساحة S= π. أ ب =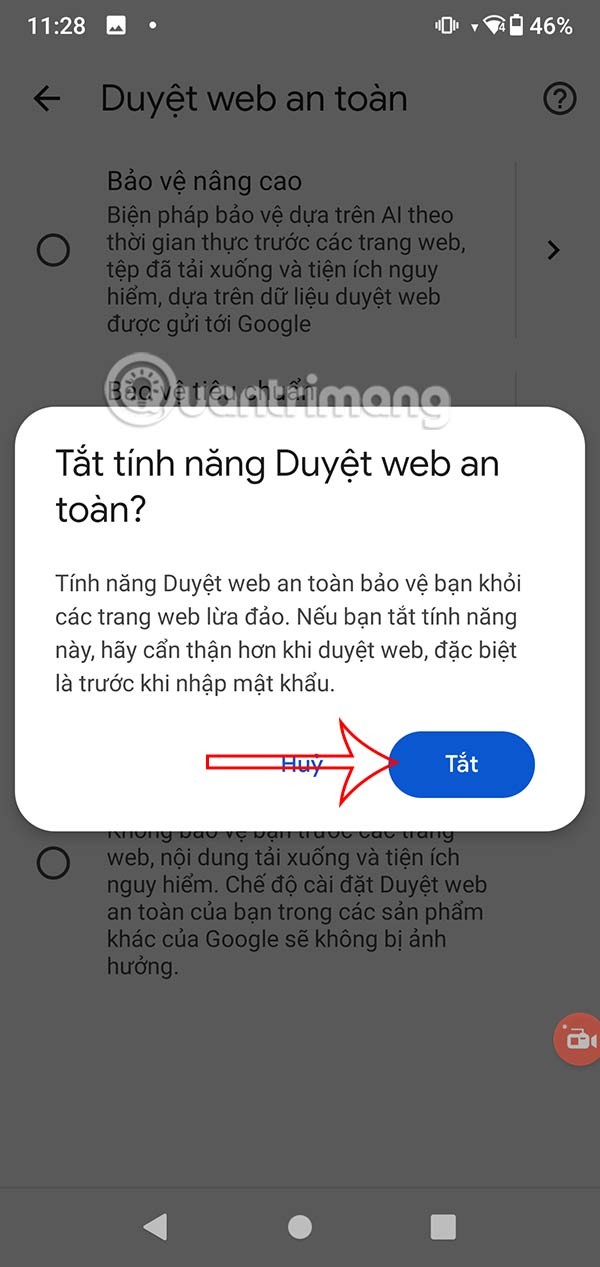
|
مثال على حساب مساحة الاسطوانة
الدرس الأول :
المساحة الجانبية للاسطوانة لها محيط قاعدة دائري مقداره 13سم وارتفاعها 3سم.
جائزة:
لدينا: محيط الدائرة C = 2R.π = 13 سم، h = 3 سم
وبالتالي فإن المساحة الجانبية للأسطوانة هي:
Sxq = 2πr.h = Ch = 13.3 = 39 (سم²)
الدرس 2 : نعطي أسطوانة ذات دائرة قاعدية نصف قطرها 6 سم، بينما يبلغ ارتفاع الأسطوانة من القاعدة إلى قمتها 8 سم. ما هي المساحة الجانبية والمساحة الكلية للاسطوانة؟
جائزة
وفقًا للصيغة، لدينا نصف الدائرة القاعدية r = 6 سم وارتفاع الأسطوانة h = 8 سم. لذلك لدينا الصيغة لحساب المساحة الجانبية للاسطوانة والمساحة الكلية للاسطوانة كما يلي:
مساحة سطح الأسطوانة = 2 × π xrxh = 2 × π × 6 × 8 = ~ 301 سم²
المساحة الكلية للأسطوانة = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 سم²
الدرس 3 : أسطوانة لها نصف قطر قاعدة 7سم ومساحة جانبية 352سم2.
وبالتالي فإن ارتفاع الأسطوانة هو:
(أ) 3.2 سم؛ (ب) 4.6 سم؛ (ج) 1.8 سم
(د) 2.1 سم؛ (هـ) نتيجة أخرى
الرجاء اختيار النتيجة الصحيحة.
الحل: لدينا
إذن الإجابة (هـ) صحيحة.
الدرس 4 : ارتفاع الأسطوانة يساوي نصف قطر دائرة القاعدة. المساحة الجانبية للأسطوانة هي 314 سم2. احسب نصف قطر الدائرة الأساسية وحجم الأسطوانة (قم بتقريب النتيجة إلى منزلتين عشريتين).
جائزة:
المساحة الجانبية للاسطوانة 314 سم2
لدينا Sxq = 2.π.rh = 314
حيث r = h
لذا 2πr² = 314 => r² ≈ 50 => r ≈ 7.07 (سم)
حجم الأسطوانة: V = π.r2.h = π.r3 ≈ 1109.65 (سم³).
نأمل أن تكون المقالة أعلاه قد ساعدتك في فهم المعرفة الأساسية والمتقدمة حول الأسطوانات، وكيفية حساب المساحة الكلية والمساحة الجانبية للأسطوانة.









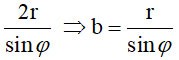
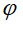 الزاوية بين محور OI و (P)
الزاوية بين محور OI و (P)











